UNIVERSIDAD AUTÓNOMA DEL ESTADO DE HIDALGO
DIRECCIÓN DE ENSEÑANZA MEDIA SUPERIOR Y TERMINAL
ESCUELA PREPARATORIA "LIC. JESUS ÁNGELES CONTRERAS"
Objetivo
- Conocer el significado de la palabra calculo
- Desarrollar un conocimiento claro del papel que juegan las matemáticas en el desarrollo de la humanidad
- Entender de forma cronológica los hechos más importantes en el desarrollo que ha vivido la ciencia de las matemáticas a lo largo de toda la historia, hasta llegar a las ciencias modernas.
- Conocer de forma clara la influencia de los distintos grupos culturales en el desarrollo del cálculo.
Introducción
La palabra
Cálculo proviene del latín calculus,
que significa contar con piedras. Precisamente desde que el hombre ve la
necesidad de contar comienza la historia del cálculo, o de las matemáticas.
Las matemáticas son una de las ciencias más
antiguas, y más útiles. El concepto de matemáticas, se comenzó a formar, desde que el hombre vio la necesidad de contar objetos, esta necesidad lo
llevó a la creación de sistemas de numeración
que inicialmente se componían con la utilización de los dedos, piernas, o
piedras. De nuevo, por la necesidad, se hizo forzosa la implementación de
sistemas más avanzados y que pudieran resolver la mayoría de los problemas que se presentaban con continuidad.
El cálculo
constituye una de las grandes conquistas intelectuales de la humanidad.
El cálculo
cristaliza conceptos y métodos que la humanidad ha tratado de dominar por más
de veinte siglos.
Hasta el
siglo XVII se pudo trabajar con los métodos “infinitesimales” para tener la
madurez social, científica y matemática que permitiría construir el Cálculo que
utilizamos en nuestros días.
Para el desarrollo de este proceso se contaba con:
el álgebra, las técnicas de cálculo, variables, problemas de cuadraturas,
búsqueda de tangentes, etc. Las causas fueron las exigencias de la mecánica, la
astronomía y la física. Sus aplicaciones son difíciles de cuantificar porque
toda la matemática moderna ha recibido su influencia.
El
extraordinario avance registrado por la matemática, la física y la técnica
durante los siglos XVIII, XIX y XX, se lo debemos al Cálculo infinitesimal. Por
eso se considera como una de las joyas de la creación.
Civilizaciones antiguas
La
Civilización Egipcia llevaba la pauta con el avance en sus conocimientos matemáticos.
Según varios papiros escritos en esa época, los egipcios inventaron el primer
sistema de numeración.
Otras
civilizaciones importantes en la historia, como la babilónica, crearon otros
sistemas de numeración.
En la China
Antigua y la India Antigua, utilizaron un sistema decimal jeroglífico.
Grecia
Las
matemáticas obtuvieron su mayor aporte en la cultura Greco Romana. En Grecia se
hizo popular la creación de escuelas donde grandes pensadores daban resolución
a problemas de geometría, algebra y trigonometría.
En la geometría
se dio la demostración del teorema de Pitágoras, que fue hallado el método para
conseguir la seria indefinida de ternas de números pitagóricos.
Demócrito y
otros grandes pensadores intentan dar respuestas con la unificación de las
matemáticas y la teoría filosófica atomicista.
Grecia se
considera como la cuna de esta ciencia, y la época es comprendida como la edad de Oro de las matemáticas.
Cultura Árabe
Los avances obtenidos en esta época, enmarcan
al concepto del límite, la introducción de los números racionales e irracionales, especialmente
los reales positivos, y el desarrollo en la trigonometría, en donde se
construyeron tablas trigonométricas de alta exactitud.
En sus comienzos el
cálculo fue desarrollado para estudiar cuatro problemas científicos y
matemáticos:
- Encontrar la tangente a una curva en un punto.
- Encontrar el valor máximo o mínimo de una cantidad.
- Encontrar la longitud de una curva, el área de una región y el volumen de un sólido.
- Dada una fórmula de la distancia recorrida por un cuerpo en cualquier tiempo conocido, encontrar la velocidad y la aceleración del cuerpo en cualquier instante. Recíprocamente, dada una fórmula en la que se especifique la aceleración o la velocidad en cualquier instante, encontrar la distancia recorrida por el cuerpo en un período de tiempo conocido.
En parte estos
problemas fueron analizados por las mentes más brillantes de este siglo,
concluyendo en la obra cumbre del filósofo-matemático alemán Gottfried Wilhelm
Leibniz y el físico-matemático inglés Isaac Newton: la creación del cálculo.
Primeros Matemáticos
Es
considerado uno de los principales precursores del álgebra. Utiliza la
geometría como medio para resolver problemas algebraicos, fundando lo que el
llamo: Logística especiosa; el arte del cálculo sobre símbolos.
La logística especiosa
La logística especiosa
Los matemáticos del Renacimiento se sentían continuadores de las matemáticas griegas, que son fundamentalmente geometría. En la época de Viète el álgebra, derivada de la aritmética, se percibe sólo como un catálogo de reglas. Algunos matemáticos, entre los que se cuenta Cardan en 1545, utilizaban razonamientos geométricos para justificar métodos algebraicos.
Así, la geometría parecía ser un instrumento seguro y potente para resolver cuestiones algebraicas, pero la utilización del álgebra para resolver problemas geométricos parecía mucho más problemática. Y, sin embargo, ésa era la propuesta de Viète.
A partir de 1591, Viète, que era muy rico, empezó a publicar a sus expensas la exposición sistemática de su teoría matemática, a la que llama logística especiosa (de specis: símbolo) o arte del cálculo sobre símbolos.
La logística especiosa procede en tres tiempos:
- En un primer tiempo, se anotan todas las magnitudes presentes, así como sus relaciones, utilizando un simbolismo adecuado que Viète había desarrollado. A continuación, se resume el problema en forma de ecuación. Viète llama a esta etapa la zetética. Escribe las magnitudes conocidas como consonantes (B, D, etc.) y las magnitudes desconocidas como vocales (A, E, etc.).
- El análisis porístico permite a continuación transformar y discutir la ecuación. Se trata de encontrar una relación característica del problema, la porisma, a partir de la cual se pueda pasar a la siguiente etapa.
- En la última etapa, el análisis rético, volvemos al problema inicial del que exponemos una solución por medio de una construcción geométrica basada en la porisma.
Entre los problemas que Viète aborda con este método, hay que citar la resolución completa de las ecuaciones de segundo grado de forma 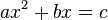 y de las ecuaciones de tercer grado de forma
y de las ecuaciones de tercer grado de forma 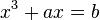 con
con  y
y  positivos (Viète pone los cambios de variable sucesivos:
positivos (Viète pone los cambios de variable sucesivos:  y
y  llevándolo de ese modo a una ecuación de segundo grado)
llevándolo de ese modo a una ecuación de segundo grado)
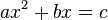 y de las ecuaciones de tercer grado de forma
y de las ecuaciones de tercer grado de forma 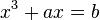 con
con  y
y  positivos (Viète pone los cambios de variable sucesivos:
positivos (Viète pone los cambios de variable sucesivos:  y
y  llevándolo de ese modo a una ecuación de segundo grado)
llevándolo de ese modo a una ecuación de segundo grado)
Posteridad de la logística especiosa
La logística especiosa tuvo una posteridad muy limitada. Viète no era el primero que proponía la notación de cantidades desconocidas con letras. Además, sus notaciones matemáticas son muy pesadas, y su desarrollo algebraico, que no consigue separar con claridad álgebra y geometría hace necesario un largo desarrollo en los problemas más complejos. Su álgebra se olvidó pronto, apartada por la geometría cartesiana.
Sin embargo fue el primero que introdujo la notación para los datos de un problema (y no sólo para las incógnitas), y se dio cuenta de la relación existente entre las raíces y los coeficientes de un polinomio.
La principal originalidad de Viète consistió en afirmar el interés de los métodos algebraicos y en tratar de hacer una exposición sistemática de dichos métodos. No dudó en afirmar que gracias al álgebra se podrán resolver todos los problemas (Nullum non problema solvere).
Desarrollo del cálculo diferencial con un método que
consistía en estudiar una curva mediante otras curvas más sencillas que pasaban
por arriba y por debajo de la curva en estudio.
Fermat fue junto con René Descartes uno de los principales matemáticos de la primera mitad del siglo XVII.
Fermat es uno de los pocos matemáticos que cuentan con un asteroide con su nombre, (12007) Fermat. También se le ha dado la denominación de Fermat a un cráter lunar de 39 km de diámetro.
Descubrió el cálculo diferencial antes que Newton y Leibniz, fue cofundador de la teoría de probabilidades junto a Blaise Pascal e independientemente de Descartes, descubrió el principio fundamental de la geometría analítica. Sin embargo, es más conocido por sus aportaciones a la teoría de números en especial por el conocido como último teorema de Fermat, que preocupó a los matemáticos durante aproximadamente 350 años, hasta que fue demostrado en 1995 por Andrew Wiles ayudado por Richard Taylor.
Fermat fue junto con René Descartes uno de los principales matemáticos de la primera mitad del siglo XVII.
Fermat es uno de los pocos matemáticos que cuentan con un asteroide con su nombre, (12007) Fermat. También se le ha dado la denominación de Fermat a un cráter lunar de 39 km de diámetro.
Descubrió el cálculo diferencial antes que Newton y Leibniz, fue cofundador de la teoría de probabilidades junto a Blaise Pascal e independientemente de Descartes, descubrió el principio fundamental de la geometría analítica. Sin embargo, es más conocido por sus aportaciones a la teoría de números en especial por el conocido como último teorema de Fermat, que preocupó a los matemáticos durante aproximadamente 350 años, hasta que fue demostrado en 1995 por Andrew Wiles ayudado por Richard Taylor.
Newton y Leibniz
Una de las más grandes controversias en las que Newton se vio envuelto fue la de la paternidad del "cálculo infinitesimal". Leibniz y sus seguidores defendieron la anterioridad de su obra respecto a la de Newton, y este último y sus partidarios, señalaron la posibilidad de plagio por parte del primero. Las discusiones y acusaciones mutuas duraron años en vida de estos dos personajes históricos y continuaron con posterioridad de la mano de sus seguidores. A pesar de ello y de que los debates fueron duros y con malos modos por parte de Newton, parece que las relaciones profesionales entre ambos destacados matemáticos y científicos no llegaron a interrumpirse.
En línea con esa defensa de sus descubrimientos que Newton tuvo que hacer en su vida, cabe mencionar el enfrentamiento internacional con Gottfried Wilhelm Leibniz (1646 - 1716), el gran filósofo, matemático, jurista, bibliotecario y político alemán, contemporáneo de Newton casi matemáticamente. Quiero decir que Leibniz nació cuatro años más tarde que nuestro autor (1646) y murió once años antes (1716). Este gran personaje alemán fue un excelso matemático e inventó el cálculo infinitesimal (decimal o integral) en paralelo con Newton y quizás antes, aunque una cosa es la primera vez que se inventa algo y otra la primera vez que se publica. A este respecto ya hemos dicho en varias ocasiones lo que Newton se resistía a dar a conocer su pensamiento y sus aportaciones.
Son
considerados los inventores del cálculo. Fueron ellos quienes dieron a los
procedimientos infinitesimales de sus antecesores, Barrow y Fermat, la unidad
algorítmica y la precisión necesaria como método novedoso y de generalidad
suficiente para su desarrollo posterior.
Los métodos
enfatizaron la experiencia empírica y la descripción matemática de nuestra
relación con la realidad.
Ambos
descubrieron este cálculo en forma independiente y casi simultánea.
Descubrió el cálculo integral, describió la relación recíproca entre los
cálculos diferencial integral. Sus
trabajos están motivados por sus propias investigaciones físicas.
De 1667 a 1669 emprendió investigaciones sobre óptica y fue elegido fellow del Trinity College. En 1669 su mentor, Isaac Barrow, renunció a su Cátedra Lucasiana de matemática, puesto en el que Newton le sucedería hasta 1696. El mismo año envió a John Collins, por medio de Barrow, su "Analysis per aequationes número terminorum infinitos". Para Newton, este manuscrito representa la introducción a un potente método general, que desarrollaría más tarde: su cálculo diferencial e integral.
Newton había descubierto los principios de su cálculo diferencial e integral hacia 1665-1666 y, durante el decenio siguiente, elaboró al menos tres enfoques diferentes de su nuevo análisis.
Newton y Leibniz protagonizaron una agria polémica sobre la autoría del desarrollo de esta rama de la matemática. Los historiadores de la ciencia consideran que ambos desarrollaron el cálculo independientemente, si bien la notación de Leibniz era mejor y la formulación de Newton se aplicaba mejor a problemas prácticos. La polémica dividió aún más a los matemáticos británicos y continentales, sin embargo esta separación no fue tan profunda como para que Newton y Leibniz dejaran de intercambiar resultados.
Newton abordó el desarrollo del cálculo a partir de la geometría analítica desarrollando un enfoque geométrico y analítico de las derivadas matemáticas aplicadas sobre curvas definidas a través de ecuaciones. Newton también buscaba cómo cuadrar distintas curvas, y la relación entre la cuadratura y la teoría de tangentes. Después de los estudios de Roberval, Newton se percató de que el método de tangentes podía utilizarse para obtener las velocidades instantáneas de una trayectoria conocida. En sus primeras investigaciones Newton lidia únicamente con problemas geométricos, como encontrar tangentes, curvaturas y áreas utilizando como base matemática la geometría analítica de Descartes. No obstante, con el afán de separar su teoría de la de Descartes, comenzó a trabajar únicamente con las ecuaciones y sus variables sin necesidad de recurrir al sistema cartesiano.
Después de 1666 Newton abandonó sus trabajos matemáticos sintiéndose interesado cada vez más por el estudio de la naturaleza y la creación de sus Principia.
Escribió un manuscrito usando por
primera vez la anotación f(x).dx con el signo integral y da la regla de la
diferenciación de un producto. Descubre la el diferencial de la potencia:
d(xn)=nx-1dx para n entero y fraccionario. A diferencia de newton, Leibniz
conserva un carácter mas geométrico y trata a la derivada como un cociente
incremental. Habla de incrementos infinitamente pequeños, a los que llama
diferenciales.
Lo que
Newton llamo fluxión, para Leibniz fue cociente de diferenciales (dy/dx).
El calculo de Leibniz fue ligeramente mejor de el que Newton.
Fue un filósofo,matemático, bibliotecario y político alemán. Fue uno de los grandes pensadores de los siglos XVII y XVIII, y se le reconoce como "El último genio universal". Realizó profundas e importantes contribuciones en las áreas de metafísica, epistemología, lógica, filosofía de la religión, así como a la matemática, física, geología, jurisprudencia e historia
El calculo de Leibniz fue ligeramente mejor de el que Newton.
Fue un filósofo,matemático, bibliotecario y político alemán. Fue uno de los grandes pensadores de los siglos XVII y XVIII, y se le reconoce como "El último genio universal". Realizó profundas e importantes contribuciones en las áreas de metafísica, epistemología, lógica, filosofía de la religión, así como a la matemática, física, geología, jurisprudencia e historia
Escribió el
primer libro de cálculo diferencial, L'Analyse des Infiniment Petits pour l'Intelligence des Lignes Courbes(Análisis de los infinitamente pequeños para el entendimiento de las líneas curvas). Gran parte del contenido de este libro se
basó en el trabajo de Juan Bernoulli.
El logro más conocido atribuído a su nombre es el descubrimiento de la regla de L'Hôpital, que se emplea para calcular el valor límite de una fracción donde numerador y denominador tienden a cero o ambos tienden a infinito.
Brook Taylor
En su Methodus Incrementorum Directa et Inversa (Londres, 1715) desarrolló una nueva parte dentro de la investigación matemática, que hoy se llamacálculo de las diferencias finitas. Entre las distintas aplicaciones, se usó para determinar la forma del movimiento de una cuerda vibrante, reducido por él por vez primera con éxito a principios mecánicos. El mismo trabajo contenía la famosa fórmula conocida como Teorema de Taylor, cuya importancia sólo se reconoció en 1772, cuando Lagrange se dio cuenta de su valor y lo definió como "el diferencial principal del fundamento del cálculo".
En su Ensayo sobre la prospectiva lineal (Londres, 1715) Taylor expresó los verdaderos principios de la prospectiva de modo más original y general que los anteriores; pero el trabajo tuvo algún problema por su brevedad y su oscuridad, defectos que se pueden aplicar a la mayor parte de sus obras; este trabajo necesitó el perfeccionamiento que desarrollaron Joshua Kirby (1754) y Daniel Fournier (1761).
Taylor fue elegido miembro de la Royal Society a principios de 1712 y el mismo año pasó a formar parte del comité para el juicio sobre reclamos de SirIsaac Newton y Gottfried Leibniz; desde el 13 de enero de 1714 al 21 de octubre a 1718 fue secretario de la sociedad.
El siglo XVII
Durante
buena parte del siglo los discípulos de Newton y Leibniz se basaron en sus
trabajos para resolver diversos problemas de física, astronomía e ingeniería.
A los matemáticos de fines del siglo el horizonte matemático les parecía obstruido. Los sabios sentían la necesidad de estudiar conceptos nuevos y hallar nuevos procedimientos.
Los hermanos Bernoulli
Inventaron el cálculo de variaciones y el matemático francés
Monge la geometría descriptiva.
En su libro Ars Conjectandi, publicado en 1713 y que se considera como el primer volumen substancial en la teoría de probabilidad, formuló el principio básico de teoría de probabilidad que se conoce como Teorema de Bernoulli o Ley de los grandes números: si la probabilidad de algún evento dado es p y si se han hecho n intentos independientes con k éxitos, entonces k / n p conforme n . Este teorema fue el primer intento para deducir medidas estadísticas a partir de probabilidades individuales y Bernoulli tardó veinte años en perfeccionarlo. Para poder dar una idea de la importancia del resultado de Bernoulli y los problemas que lo rodean, habría que extenderse y exponer varios puntos.
En 1690 sugirió el nombre “integral” a Leibniz y puntualizó que en un punto máximo o mínimo la derivada de la función no tiene que anularse; sino que puede tomar un “valor infinito” o asumir una forma indeterminada. En su primer artículo sobre series infinitas, en 1689, presentó la “desigualdad de Bernoulli”: (1 + x)n > 1 + nx
En su libro Ars Conjectandi, publicado en 1713 y que se considera como el primer volumen substancial en la teoría de probabilidad, formuló el principio básico de teoría de probabilidad que se conoce como Teorema de Bernoulli o Ley de los grandes números: si la probabilidad de algún evento dado es p y si se han hecho n intentos independientes con k éxitos, entonces k / n p conforme n . Este teorema fue el primer intento para deducir medidas estadísticas a partir de probabilidades individuales y Bernoulli tardó veinte años en perfeccionarlo. Para poder dar una idea de la importancia del resultado de Bernoulli y los problemas que lo rodean, habría que extenderse y exponer varios puntos.
En 1690 sugirió el nombre “integral” a Leibniz y puntualizó que en un punto máximo o mínimo la derivada de la función no tiene que anularse; sino que puede tomar un “valor infinito” o asumir una forma indeterminada. En su primer artículo sobre series infinitas, en 1689, presentó la “desigualdad de Bernoulli”: (1 + x)n > 1 + nx
Hermanos Bernoulli Monge
Francés, dio un tratamiento
completamente analítico de la mecánica, realizó contribuciones al estudio de
las ecuaciones diferenciales y la teoría de números, y desarrolló la teoría de
grupos.
Lagrange desproveyó al estudio de las derivadas de cualquier cosa que hablara defluxiones, cantidades infinitamente pequeñas o infinitésimos. Suyo es el término “derivada” y la notación x’ que utilizamos actualmente para designar la derivada de una función. También fueron importantes sus aportaciones a la Teoría de Números y la resolución de ecuaciones algebraicas, que sentarían las bases para la futura teoría de grupos.
Notaciones de Lagrange y´ o f´(x)
Son de la forma y = x f(y') + g(y') donde f(y') no puede ser igual y'.
Se resuelven derivando y llamando y' = p con lo que obtenemosp = f(p) + [x f'(p) + g'(p)]p' esta ecuación es lineal y se integra tomando x como función de p.Ecuación de Lagrange:y + xϕ (y')+ ψ (y’)=0.
Su contemporáneo Laplace escribió Teoría analítica de las probabilidades (1812) y el clásico Mecánica celeste (1799-1825), que le valió el sobrenombre de "el Newton francés".
Se resuelven derivando y llamando y' = p con lo que obtenemosp = f(p) + [x f'(p) + g'(p)]p' esta ecuación es lineal y se integra tomando x como función de p.Ecuación de Lagrange:y + xϕ (y')+ ψ (y’)=0.
Su contemporáneo Laplace escribió Teoría analítica de las probabilidades (1812) y el clásico Mecánica celeste (1799-1825), que le valió el sobrenombre de "el Newton francés".
Laplace
Escribió Teoría analítica de las probabilidades y el clásico Mecánica
celeste,
que le valió el sobrenombre de "el Newton francés".
Sin
embargo el gran matemático del siglo fue el suizo Euler, quien aportó ideas
fundamentales sobre el cálculo y otras ramas de las matemáticas y sus
aplicaciones. Euler escribió textos sobre cálculo, mecánica y álgebra que se
convirtieron en modelos a seguir.
El
tratamiento de LaGrange era completamente algebraico y basado en el concepto de
las series infinitas.
Leonhard Euler
Aportó ideas fundamentales sobre el cálculo y otras ramas de
las matemáticas y sus aplicaciones. Euler escribió textos sobre cálculo,
mecánica y álgebra que se convirtieron en modelos a seguir para otros autores
interesados en estas disciplinas. El éxito de Euler y de otros matemáticos para
resolver problemas tanto matemáticos como físicos utilizando el cálculo sólo
sirvió para acentuar la falta de un desarrollo adecuado y justificado de las
ideas básicas del cálculo. La teoría de Newton se basó en la cinemática y las
velocidades, la de Leibniz en los infinitésimos, y el tratamiento de LaGrange
era completamente algebraico y basado en el concepto de las series infinitas.
Todos estos sistemas eran inadecuados en comparación con el modelo lógico de la
geometría griega, y este problema no fue resuelto hasta el siglo posterior.
El siglo XIX
Un problema
importante fue definir el significado de la palabra función. Euler, Lagrange y el matemático francés
Fourier aportaron soluciones, pero
fue el matemático alemán Dirichlet quien
propuso su definición en los términos actuales.
Alemán, propuso su definición en los términos actuales de la palabra función.
En 1821.
Consiguió un enfoque lógico y apropiado del cálculo y se dedicó a dar una definición precisa de "función continua". Basó su visión del cálculo sólo en cantidades finitas y el concepto de límite.
Realizó aportes relevantes en:
- Campo de la teoría de los números.
- Estableció criterios de convergencia para las series.
- Desarrolló la teoría de las series de Fourier.
- Demostración particular del teorema de Fermat
- Aplicó las funciones analíticas al cálculo de problemas aritméticos
- En el campo del análisis matemático perfeccionó la definición y concepto de función
- En mecánica teórica se centró en el estudio del equilibrio de sistemas y la teoría potencial newtoniano que lo llevó a lo que se conoce como el problema de Dirichlet.
- En 1852 estudió el problema de una esfera colocada en un fluido incompresible, en el curso de esta investigación se convierte en la primera persona para integrar las ecuaciones hidrodinámicas exactamente.
Agustin Louis Cauchy
Consiguió un enfoque lógico y apropiado del cálculo y se dedicó a dar una definición precisa de "función continua". Basó su visión del cálculo sólo en cantidades finitas y el concepto de límite.
En 1811, Cauchy resolvió el problema de Poinsot, generalización del teorema de Euler sobre los poliedros. Un año más tarde, publicaría una memoria sobre el cálculo de las funciones simétricas y el número de valores que una función puede adquirir cuando se permutan de todas las maneras posibles las cantidades que encierra. En 1814, apareció su memoria fundamental sobre las integrales definidas y luego abordando el teorema de Fermat sobre los números poligonales, llegó a demostrarlo, cosa que no pudieron Euler, Legendre, Lagrange, ni Gauss. Uno de los mayores triunfos lo obtuvo dando vigor a las demostraciones de Lagrange, ateniéndose al cálculo de ceros e infinitos y fijando las convergencias de las series del análisis. Algunas de sus obras relacionadas con el cálculo son el Traité de calcul diferentiel et integral (Tratado del cálculo diferencial e integral), Leçons sur la aplication du calcul infinitesimal á la géometrie (Lecciones sobre la aplicación del cálculo infinitesimal a la geometría), Sur les integrales definies prises entre des limites imaginaires (Sobre las integrales definidas tomadas entre límites imaginarios), Sur la aplication du calcul des residus á la solution des problèmes des Physique matématique (Sobre la aplicación del cálculo a la resolución de problemas físico-matemáticos), y Sur un nouveau calcul des limites (Sobre un nuevo cálculo de límites). No dejó de ser productivo intelectualmente ni al final de su vida, pues días antes de su muerte leyó en el Instituto una memoria sobre el empleo de un artificio de cálculo llamado coeficiente regulador.
Quien encontró una definición adecuada para los números reales.
Dedekind aprendió matemáticas en los departamentos de matemáticas y física de aquella universidad, siendo uno de sus principales profesores Moritz Abraham Stern, y también física de la mano de Wilhelm Eduard Weber. Su tesis doctoral, supervisada por Gauss, se titulaba Über die Theorie der Eulerschen Integrale (Sobre la teoría de las Integrales eulerianas), y aunque en ella no se reflejaba el talento que mostró en sus trabajos posteriores, Gauss supo apreciar el don de Dedekind para las matemáticas. Dedekind recibió su doctorado en 1852, siendo el último alumno de Gauss, y trabajó a continuación en una tesis de habilitación, que era necesaria en Alemania para obtener la "venia docendi" (habilitación de enseñanza docente en universidades alemanas).
Durante los siguientes años, estudió la teoría de los números y otras materias con Gustav Dirichlet, al que le uniría una gran amistad. Para ampliar sus conocimientos, abordó el estudio de las funciones abelianas y elípticas de la mano del genial Bernhard Riemann. Sólo tras estas experiencias, en su formación, encontró al fin sus campos de trabajo principales: el álgebra y la teoría de números algebraicos. Se dice de él que fue el primero en impartir clases universitarias sobre la teoría de las ecuaciones de Galois. Fue además el primero en comprender el significado fundamental de las nociones degrupo, cuerpo, ideal en el campo del álgebra, la teoría de números y la geometría algebraica.
Uno de los más importantes matemáticos de la historia, dio una explicación
adecuada del concepto de número complejo; estos números formaron un nuevo y
completo campo del análisis, desarrollado en los trabajos de Cauchy,
Weierstrass y el matemático alemán Riemann.
Una de las mayores aportaciones al cálculo integral que realizó Gauss, fue la introducción de esta función, conocida más comúnmente como la Campana de Gauss.
Esta distribución es frecuentemente utilizada en las aplicaciones estadísticas. Su propio nombre indica su extendida utilización, justificada por la frecuencia o normalidad con la que ciertos fenómenos tienden a parecerse en su comportamiento a esta distribución.Muchas variables aleatorias continuas presentan una función de densidad cuya gráfica tiene forma de campana.En otras ocasiones, al considerar distribuciones binomiales, tipo B(n,p), para un mismo valor de p y valores de n cada vez mayores, se ve que sus polígonos de frecuencias se aproximan a una curva en "forma de campana".En resumen, la importancia de la distribución normal se debe principalmente a que hay muchas variables asociadas a fenómenos naturales que siguen el modelo de la normal
Aquí está la representación gráfica de la función Campana de Gauss:
Esta distribución es frecuentemente utilizada en las aplicaciones estadísticas. Su propio nombre indica su extendida utilización, justificada por la frecuencia o normalidad con la que ciertos fenómenos tienden a parecerse en su comportamiento a esta distribución.Muchas variables aleatorias continuas presentan una función de densidad cuya gráfica tiene forma de campana.En otras ocasiones, al considerar distribuciones binomiales, tipo B(n,p), para un mismo valor de p y valores de n cada vez mayores, se ve que sus polígonos de frecuencias se aproximan a una curva en "forma de campana".En resumen, la importancia de la distribución normal se debe principalmente a que hay muchas variables asociadas a fenómenos naturales que siguen el modelo de la normal
- Caracteres morfológicos de individuos (personas, animales, plantas,...) de una especie, p.ejm. tallas, pesos, envergaduras, diámetros, perímetros,...
- Caracteres fisiológicos, por ejemplo: efecto de una misma dosis de un fármaco, o de una misma cantidad de abono.
- Caracteres sociológicos, por ejemplo: consumo de cierto producto por un mismo grupo de individuos, puntuaciones de examen.
- Caracteres psicológicos, por ejemplo: cociente intelectual, grado de adaptación a un medio,...
- Errores cometidos al medir ciertas magnitudes.
- Valores estadísticos muestrales, por ejemplo : la media.
Aquí está la representación gráfica de la función Campana de Gauss:
Fourier
Otro
importante avance fue el estudio de las sumas infinitas de expresiones con
funciones trigonométricas, herramientas muy útiles tanto en las matemáticas
puras como en las aplicadas.
Tras las victorias británicas y la capitulación de los franceses al mando del general Menou en 1801, Fourier volvió a Francia, donde fue nombrado prefecto del departamento de Isère, y empezó sus experimentos sobre la propagación del calor. Se trasladó a París en 1816, y en 1822 publicó Teoría analítica del calor, basándose en parte en la ley del enfriamiento de Newton.
A partir de esta teoría desarrolló la denominada «serie de Fourier», de notable importancia en el posterior desarrollo del análisis matemático, y con interesantes aplicaciones a la resolución de numerosos problemas de física (más tarde, Dirichlet consiguió una demostración rigurosa de diversos teoremas que Fourier dejó planteados). Dejó inacabado su trabajo sobre resolución de ecuaciones, que se publicó en 1831 y que contenía una demostración de su teorema sobre el cálculo de las raíces de una ecuación algebraica.
Estudió los conjuntos
infinitos y una aritmética de números infinitos. La teoría de Cantor fue
considerada demasiado abstracta y criticada.
Encontramos aquí un espíritu crítico en la elaboración de estas nociones tan ricas. Esto constituye un punto de vista muy diferente del que animaba a los matemáticos del siglo anterior. Ya no se trata de construir expresiones ni forjar nuevos métodos de cálculo, sino de analizar conceptos considerados hasta entonces intuitivos.
Encontramos aquí un espíritu crítico en la elaboración de estas nociones tan ricas. Esto constituye un punto de vista muy diferente del que animaba a los matemáticos del siglo anterior. Ya no se trata de construir expresiones ni forjar nuevos métodos de cálculo, sino de analizar conceptos considerados hasta entonces intuitivos.
En
este siglo se pasa del estudio simple de los polinomios al estudio de la
estructura de sistemas algebraicos.
Boole
Para el público más amplio Boole era conocido sólo como el autor de numerosos trabajos abstrusos en temas de matemáticas, y de distintas publicaciones que se han convertido en obras. Su primer trabajo publicado fue "Investigaciones en la teoría de las transformaciones de análisis, con una aplicación especial a la reducción de la ecuación general de segundo orden."
Siglo XX
Lebesgue
Aporte
referido a la integración y a la teoría de la medida y
las modificaciones.
Lebesgue es fundamentalmente conocido por sus aportes a la teoría de la medida y de la integral. A partir de trabajos de otros matemáticos como Émile Borel y Camille Jordan, Lebesgue realizó importantes contribuciones a la teoría de la medida en 1901. Al año siguiente, en su disertación Intégrale, longueur, aire (Integral, longitud, área) presentada en la Universidad de Nancy, definió la integral de Lebesgue, que generaliza la noción de la integral de Riemann extendiendo el concepto de área bajo una curva para incluir funciones discontinuas. Este es uno de los logros del análisis moderno que expande el alcance del análisis de Fourier.
También aportó en ramas como la topología, la teoría del potencial y el análisis de Fourier. En 1905 presentó una discusión sobre las condiciones que Lipschitz que Jordan habían utilizado para asegurar que f(x) es la suma de su serie de Fourier.
A partir de 1910 no se concentró más en el área de estudio que él había iniciado, debido a que su trabajo era una generalización, y él era temeroso de las mismas. En sus palabras: Reducida a teorías generales, las matemáticas serían una forma hermosa sin contenido. Morirían rápidamente. A pesar de que desarrollos posteriores demostraron que su temor no tenía fundamentos, éste nos permite entender el curso que siguió su trabajo.
En la
Conferencia Internacional de Matemáticos que tuvo lugar en París en 1900, el
matemático alemán David Hilbert
Contribuyó de forma sustancial en casi
todas las ramas de la matemática retomó veintitrés problemas matemáticos que él
creía podrían ser las metas de la investigación matemática.
El
avance originado por la invención del ordenador o computadora digital
programable dio un gran impulso a ciertas ramas de la matemática, como el
análisis numérico y las matemáticas finitas.
Se
convirtió en una poderosa herramienta en campos como el estudio de los algoritmos como la teoría de números, las ecuaciones
diferenciales y el álgebra abstracta. Además, permitió encontrar la solución a
varios problemas matemáticos que no se habían podido resolver anteriormente.
Teorías
distintas se han reunido para formar teorías más completas y abstractas.
CALCULO DIFERENCIAL
Cuando surgen cuestiones concernientes a la razón entre
dos cantidades variables, entramos en los dominios del Cálculo Diferencial. Son
por tanto objeto de estudio del cálculo diferencial temas como la velocidad (razón
entre la distancia recorrida y el tiempo empleado en recorrerla) de una
partícula en un momento determinado, la pendiente (razón entre la diferencia de
las ordenadas y las abscisas de dos puntos en el plano cartesiano) de la recta
tangente a una gráfica en un punto dado de ésta, etc.
Incrementos: cuando una cantidad variable
pasa de un valor inicial a otro valor, se dice que ha tenido un incremento.
Para calcular este incremento basta con hallar la diferencia entre el valor
final y el inicial.
Derivada de una función: Sea f una función definida en todo número de algún
intervalo I, la derivada de f es aquella función,
denotada por f ', tal que su valor en cualquier número xde I,
está dado por:
f ' (x)= lim f( x+ ▲x) - f (x)
▲→0 ▲x
Se dice que una función es diferenciable o derivable cuando es posible
hallar su derivada.
El cálculo diferencial es una parte importante del análisis
matemático y dentro del mismo del cálculo. Consiste en el estudio del
cambio de las variables dependientes cuando cambian las variables
independientes de las funciones o campos objetos del análisis. El principal
objeto de estudio en el cálculo diferencial es la derivada. Una
noción estrechamente relacionada es la de diferencial de una función.
En el estudio del cambio de una
función, es decir, cuando cambian sus variables independientes es de especial
interés para el cálculo diferencial el caso en el que el cambio de las
variables es infinitesimal, esto es, cuando dicho cambio tiende a cero (se hace
tan pequeño como se desee). Y es que el cálculo diferencial se apoya
constantemente en el concepto básico del límite. El
paso al límite es la principal herramienta que permite desarrollar la teoría
del cálculo diferencial y la que lo diferencia claramente del álgebra.
Desde el punto de vista matemático de
las funciones y la geometría, la derivada de una función en un cierto punto es una medida de la tasa en la cual una función cambia conforme un argumento se modifica. Esto es, una derivada involucra, en términos matemáticos,
una tasa de cambio. Una derivada es el cálculo de las pendientes
instantáneas de f(x) en cada punto x. Esto se corresponde a las pendientes de las tangentes de la gráfica de dicha función en sus puntos (una tangente por punto); Las derivadas
pueden ser utilizadas para conocer la concavidad de una función, sus intervalos de crecimiento, sus máximos y mínimos.
La inversa de una derivada se llama primitiva, antiderivada o integral indefinida.
Diferenciación y diferenciabilidad
La Diferenciación puede ser usada para determinar el cambio que se produce como resultado de otro cambio, si está determinada una relación matemática entre dos objetos.
Una función es diferenciable en un
punto x si su derivada existe en ese punto; una función
es diferenciable en un intervalo si lo es en cada punto x perteneciente al intervalo. Si una función no
es continua en f, entonces no puede ser
diferenciable en f; sin embargo, aunque una función sea continua
en F, puede no ser diferenciable. Es decir, toda función
diferenciable en un punto F es continua en F, pero no toda función continua en
F es diferenciable en F (como f(x) = |x| es continua pero no diferenciable en x
= 0).
Definición de Derivada
Las derivadas se definen tomando el límite de la pendiente de las rectas secantes conforme
se van aproximando a la recta tangente.
Es difícil hallar directamente la pendiente de la
recta tangente de una función porque sólo conocemos un
punto de ésta, el punto donde ha de ser tangente a la función. Por ello,
aproximaremos la recta tangente por rectas secantes. Cuando
tomemos el límite de las pendientes de las secantes
próximas, obtendremos la pendiente de la recta tangente.
Para obtener estas pendientes, tomemos un número
arbitrariamente pequeño que llamaremos h. h representa
una pequeña variación en x, y puede ser tanto positivo como
negativo. La pendiente de la recta entre los puntos (x, f (x)) y (x+h) es
f(x+h)-f(x)
h
Esta expresión es un Cociente Diferencial de Newton.
La derivada de f en x es
el límite del valor del cociente diferencial conforme las líneas secantes se
acercan más a la tangente:
f '(x)= lim f(x+h)-f(x
h→0 h
h→0 h
Si la derivada de f existe en cada
punto x, podemos definir la derivada de f como
la función cuyo valor en el punto x es la derivada de f en x.
Puesto
que la inmediata sustitución de h por 0 da como resultado
una división por cero, calcular la derivada directamente puede ser poco
intuitivo. Una técnica es simplificar el numerador de modo que la h del denominador pueda
ser cancelada. Esto resulta muy sencillo con funciones polinómicas, pero para la mayoría de las funciones resulta
demasiado complicado.
Este blog ha sido creado por:
- Feregrino Lucario Sujeyrys Getssabel
- Macotela Salasar Aliz Gabriela
- Macotela Salinas Brenda Azalia
- Macotela Trejo Karyme Mariel





































No hay comentarios:
Publicar un comentario